TOOLS OF THE TRADE
“The best investment is in the tools of one’s own trade.””
As I pondered the workflow of a new large-scale piece such as a twenty-eight-minute clarinet sonata, I found myself dreading the process of calculating dozens of pitch class sets and piecing together just the right ones to create the tonal pallet for the piece. It’s a large piece and the idea of getting to minute twenty and realizing I had painted myself into a corner with a miscalculation seemed frightful. It’s no wonder that I approach the process with apprehension. It is time-consuming and full of pitfalls that can reverse weeks of work.
The Style
My work is not tonal. This comes as a surprise to many of the people that enjoy my music. To be clear, it’s not functionally tonal. Like the composers of the impressionist movement and, well, any composer that had had quite enough of the hierarchy of chords—the way one chord “wants” to go to another—I don’t necessarily follow the rules of predominant-dominant-tonic chord progressions. This is nothing new, there were—and are—plenty of composers that eschew the tired old syntax that Wagner tapped out with his three-hour operas (OK, maybe there’s some baggage left over from WWII). Besides, I kind of like being grouped in with Bartók, Berg, Coltrane, Debussy, Griffes, Hancock, Hindemith, Ravel, Reger, Schoenberg, Shorter, Stravinsky, Webern, and Zappa. (Wow, that’s a lot of dead white guys but you get the idea.)
The Process
I begin by choosing just two or three sonorities or chords. These are the basic sonic building blocks of the piece and these chords set the tone—palette? flavor? vocabulary?—of the whole piece. This is what sets the universe in which the piece exists. The chords can be manipulated—turned upside down, backwards, split into pieces, and transposed.
The next step is to create a synthetic scale from those chords by putting one after the other or intertwining them in ways that give rise to a whole array of related chords. Usually this is done by carefully ordering the pitches of the scale in a way that gives rise to related chords when the odd notes or even notes of the scale are stacked, the same way we get triads and seventh chords from major and minor scales in functionally tonal music.
I then go on to order the resulting chords (there may be half a dozen or more at this point) in a way that creates tension and relaxation. This is achieved through tracing common tones or by manipulating the order of symmetrical and asymmetrical sonorities.
It’s important to understand that when I speak of chord, I’m really speaking of patterns of distance (intervals) between the pitches. This all gets manipulated through mathematical calculation.
I’m not good at math.
It became clear that I needed a way to make these calculations quicker and perhaps see a few connections that I may have missed. It wouldn’t hurt if the process were a little fun too.
I needed a calculator that put all the structures in one place. It wasn’t in the app store. Yes, I checked! It’s just math. I could create a calculator in Microsoft Excel. Three weeks later I had it completed. Did I mention—I’m not good at math.
The completed Pitch Class Set Calculator
Glossary
This next part can get a little jargony. For those of you who didn’t pass your class in post-tonal theory, here’s a glossary.
The Pitch Class Calculator
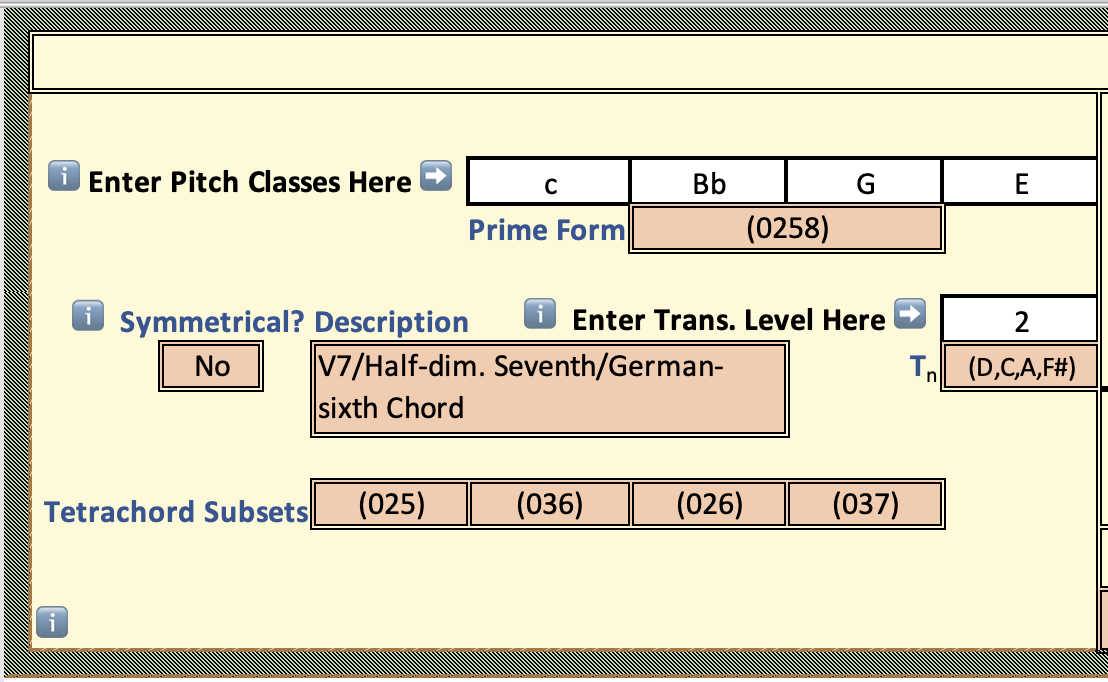
This calculator allows me to enter any three or four notes, in any order and instantly return the pitch class set. The calculator also tells me if the PCS meets my requirements for symmetry and describes the PCS in tonal terms.
The calculator will also allow me to transpose the PCS by any interval by entering the transposition level as an integer corresponding to the number of semitones. I.e., 1 = a half step and 2 = a whole step. I know, if you took my theory classes I made sure you never counted half steps, but this isn’t that kind of theory!
If I have entered a tetra chord (four pitches) it also unpacks the tetrachord into its trichord (three pitches) subsets.
Scale Analysis
Of course, I needed a calculator to analyze scales in several ways. I can enter any scale from three notes to eleven notes and instantly see information that used to take me a half hour to calculate at the piano. Why not twelve notes? I don’t write serial music and a twelve-note scale is just a chromatic scale. I’m unlikely to use that in a composition other than a special effect.
The most important tool is to see how the scales stack up. The calculator stacks up every three notes into trichords and tetrachords and returns the resulting PCSs. It does the same for every four notes. It’s worth noting that my use of the words, tertian and quartal here refer to the use of every three or four notes, not actual thirds and fourths.
The calculator will reveal the constituent trichords and tetrachords that make up the subset structure of the scale.
The calculator allows me to see the scales backwards, upside down, or backwards and upside down (retrograde, inversion, retrograde/inversion). It also allows me to rotate the scale through eleven modes and perform the same transformations on each of the resulting modes.
I can also compare all the resulting transformations of the scale by examining a list arranged by first note.
The calculator provides an analysis of all internal intervals of the scale in terms of integers representing the distance between each note.
Scale Symmetry
The calculator analyzes the internal segments of each scale for symmetry and alerts me if the scale possesses translational symmetry (▷▷), rotational symmetry (✼), or reflective symmetry (◁▷). Translational symmetry, sometimes called transpositional symmetry repeats a segment of the scale at one or more consistent intervals without changing the order or internal intervals of the segment. The calculator will tell me how many segments exist and how many notes are in each segment. Rotational symmetry rotates the interval map of the scale as if it were on a clock face to arrive at an identical interval map as the original. Reflective symmetry reverses the scale or segment of the scale. The calculator will also identify the point within the scale at which the axis of symmetry occurs.
Built For an Older, Dumber Me
The calculator includes icons (ℹ️) that tell me there is more information about a particular feature. This will come in handy as I will only use the calculator in the beginning stages of a composition and may need to be reminded about all this nerdy stuff. The whole thing is idiot proofed so I can’t inadvertently erase one of the background calculations. There are over 17,000 lines of excel data and formulas lurking just beneath the surface of this thing.
I thought it would be interesting to compare the result of entering the foundational synthetic scale and one of the pitch class sets of a recent composition to see how the calculator performs. Pretty good!
I hope you have enjoyed this explanation of my new toy. This will help me streamline my workflow in the coming months. Please come back often to read about the progression of the sonata and please consider contributing to the commissioning project.
—BLW—